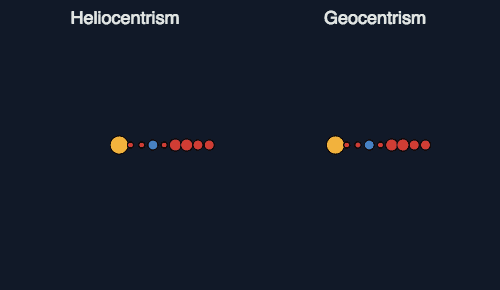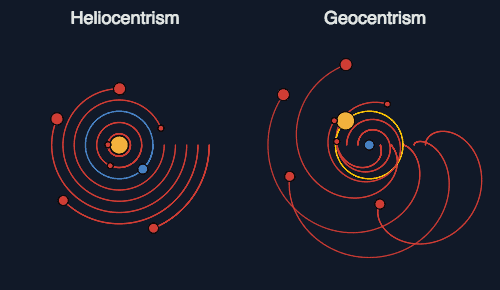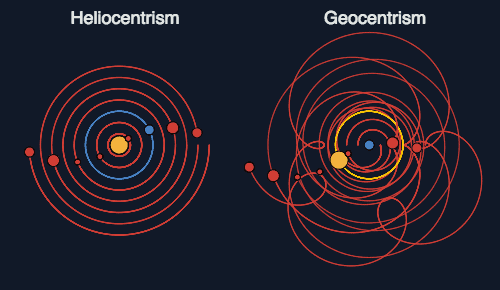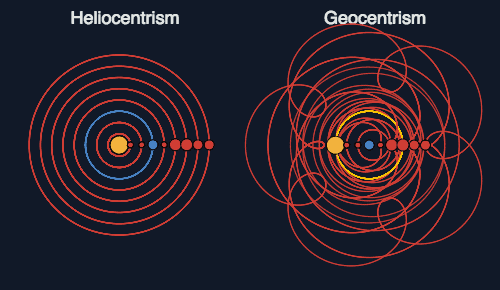
Here’s another problematic image I came across on Facebook. It was accompanied by the statement, “Heliocentrism is not necessarily the only perspective, but it is certainly the simpler one. When explanatory power is equivalent, simplicity is a powerful deciding factor.”
Can you see what is wrong with the picture?
Here’s what I wrote in a comment: “Not with circular orbits on both. That was a major reason why heliocentrism was not persuasive when first proposed. If you do not shift to elliptical orbits, then you still need epicycles to get the proposed system to fit what is observed.”
The page on Facebook then kindly responded with this: “Profile says professor of religion, but dude comes and lays down some astrophysics like a boss. Thank you for clarifying that.”
And so I concluded the conversation by saying the following: “No problem – I have a big interest in science, even though it isn’t my area of expertise. If the left had Kepler’s proposal rather than Copernicus’ then your point would have been sound – although ellipses rather than circles seemed less “simple” a solution to many in a time before Isaac Newton provided gravitational explanations for these phenomena.”
I was considering keeping this for some other time, but it fits so nicely as a complement to the previous post. It is an example of someone wanting to make a point about heliocentrism over against geocentrism, and simplicity vs. complexity, and yet not getting the facts right and thus undermining their own point by going beyond oversimplification into factual error. As Einstein is purported to have said, “Make everything as simple as possible, but not simpler.”
And so, in the interest of following the axiom as well as my own advice, I will point out that simply saying “Einstein said” would have been too simple. The saying is attributed to him, but we have no evidence that he actually said it.