I’m writing this while I’m recuperating from a concussion.
Last Saturday I had a collision with a student while doing drills at my karate class, and took a foot full force in the face while doing a backwards roll. While I felt okay immediately afterward — just a little drained — the next evening I started to get a serious headache, and for the past week I’ve been really slowed down by the aftereffects.
(I should also note that I have been bopped in the head a few times in my decades of karate training but this is by far the most serious incident. Our classes are still remarkably safe. But if you do anything for thirty years, low probability things will catch up with you eventually.)
The accident in question was my own fault — it was my responsibility to get people lined up so things like this don’t happen. But it seems to me that maybe there is a deeper lesson, at least a metaphorical one, in the error I made. So in an attempt to wring some meaning from my suffering, friends, let me present to you a tale of the dangers of…geometry. (Don’t panic! It’s only lines and angles, and no proofs or constructions will be required.)
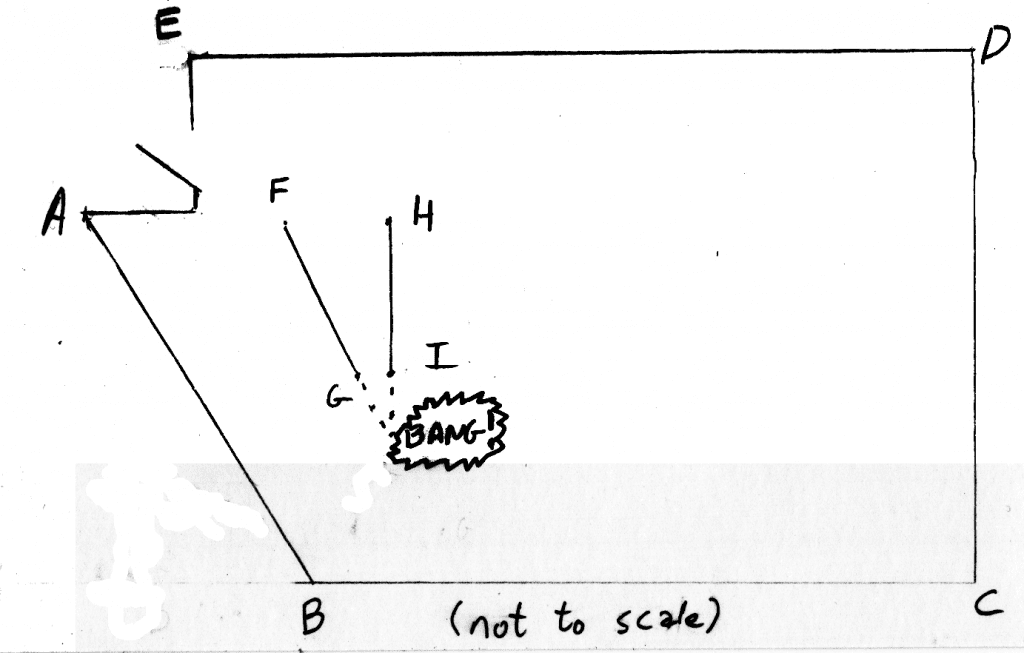
Figure 1 is a rough sketch of the room at the Y where we have class. It’s mostly rectangular except for that crazy wall AB. Most of what we do organizes neatly into straight lines and rectangles, and before this weekend, that AB wall had a set of racks against it, holding large stability balls. This left the triangle ABF sort of a no-mans land where nothing fit; it ended up being the space where people put their shoes, coats, and bags when they came in.
But this time the racks had been moved, over against the wall BC. And as AB is a mirrored wall, it became useful for us. (It’s very useful to do drills facing a mirror, not just for your own monitoring but it allows the instructor to stand behind you and see your movements from both behind and in front.) So when I took a few students to the back of the room, I lined them up facing that wall, at about the line FG, for a set of forms (kata) and solo drills.
Then we moved into a two person drill. And here’s the problem. I partnered up with one student and we set up to go back and forth along roughly line FG, parallel to the crazy wall we had just been facing. The remaining two students partnered up and took up an orientation square with the rest of the room, as we always have in the past — about on line HI.
This left us on lines that were not parallel. And Euclid will have his due — lines that are not parallel will intersect. In this case, quite forcefully.
What’s remarkable is that the collision happened because, in effect, we were operating under different sets of coordinates. I oriented my partner and myself relative to that crazy wall AB, while the other pair oriented themselves to the square portion of the room.
And neither of these is more or less correct than the other. What we had here was a collision of two world-views which were each pragmatically valid and useful on their own, but were nevertheless incompatible.
And to anyone interested in the idea that multiple “reality tunnels” can each be valid, that’s an interesting situation!
It suggests the need for buffers between spaces where different models are in effect — not because any one or another of these models is deficient, but because they lead to results that can’t both be applied at the same time.